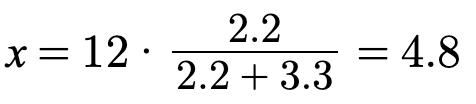Bright flashes snapping, boundless night hidden behind a fog of completion
Two years ago I ran an experiment, where for five months classes and clubs were no longer excuses I could make to myself for not spending time on passion. I took a semester off college to focus my attention on one robotics project with goals that are completely defined by me—a blank canvas, tunnel vision. Confounding variables removed, I was to answer what work I prefer and how I prefer to work. Maybe I was a little too serious.
A few breaths later, I was already graduating. Even now I feel that I am still on that gap semester; I never really went back to school after that. What I mean is, school was no longer stimulating, grades stopped being useful goals, and seemingly more rewarding things began to pull me away. Common advice recognizes this to be dangerous, so if you’re looking to do the same I should give a disclaimer: the complete freedom to explore may irreversibly change your values, and therefore what you can motivate yourself to do.
Fable #1: It’s what I imagine it would be like to hop off a bus because you spot something you really want to visit. You see the most beautiful sight of your life. Whether the bus’s destination is what you actually wanted, you won’t know because the bus has already left. But most people seem to be heading there, so you wonder whether you are missing out. The next bus won’t let you on. You are not pure.
Fable #2: It’s what I imagine it would be like following instructions to fold a complicated paper airplane, then in the middle you realize it could probably fly as is. You go off-script and improvise some folds, hold it out at arms length and admire. It flies quite far, but not as far as you wanted. You retrace to join the instructions, but the plane has too many extra creases on the wings and always curves to either side. You are not pure.
Fable #3: It’s what I imagine it would be like going to thread a needle, then you realize you want to put some beads on the thread first, but now the end of the thread has frayed, and now there are some stubborn strands that miss the eye no matter how many times you retry. You are not pure. People then tell you it’s the same thing if you put the beads on after you thread the needle.
I had intended to write about that semester right after it ended, when I was to return to taking classes. It’s been two summers since then—everyday procrastination was definitely a factor, but I also didn’t have anything direct to share. I did not learn to be more productive or more motivated in general (maybe the opposite). For things I did learn, they are hard to shape into words, and unclear whether they should be recorded neatly as truth or scribbled as diary entries to be forgotten. Either way, the context of the situation would be flattened out. It took so long also because this essay felt at the same time expected and purposeless: I had promised a follow-up on what I had learned, but now that I am supposedly learned, selfishly, I feel no intrinsic drive to define and distill advice; actually, one of the opinions I have strengthened the most during this period is that problems are best nursed case-by-case, that general statements are either obvious, weak, or wrong.
Anyway, I tried to write down some things I learned.
TLDR:
Abstractions reduce detail to combat complexity
School teaches multi-level pattern matching
Multi-level similarity search is the same concept but more powerful
Language is limited, so harder to teach ≠ harder to learn
Alternating between abstractions can unblock creativity
Art helps us find what we want to optimize
Abstractions reduce detail to combat complexity
Logic and the digital computers that encode it are so powerful because binary rejects noise like nothing else. Transistors are designed so that microscopic effects pull something close to OFF to become OFF and pull something close to ON to become ON, like a light switch that refuses to stay in the middle, or a magnet between two separated pieces of steel. A spectrum becomes two points, and even consistent disturbances (below a certain predictable threshold) cannot affect the result.
Continuous variables on the other hand, like most things we can sense, compound error and drift. Filling a measuring cup with 1 cup of water a thousand times, there’s a good chance you would have actually measured something that looks like 1003.487928362 cups of water in the end. How can you say that anything is equal to anything else?
Computers are reliable not because they are automated, but because they are designed so there exists a way for errors not to build up, and that ability to compound is what enables the automation. You can build long chains of modules because each link can be reliably made quite strong. The model of each component can be almost certainly correct, and so the model of a whole system of components working together can be quite strong too, to the point where a model of the system is functionally equivalent to the system itself with all the context.
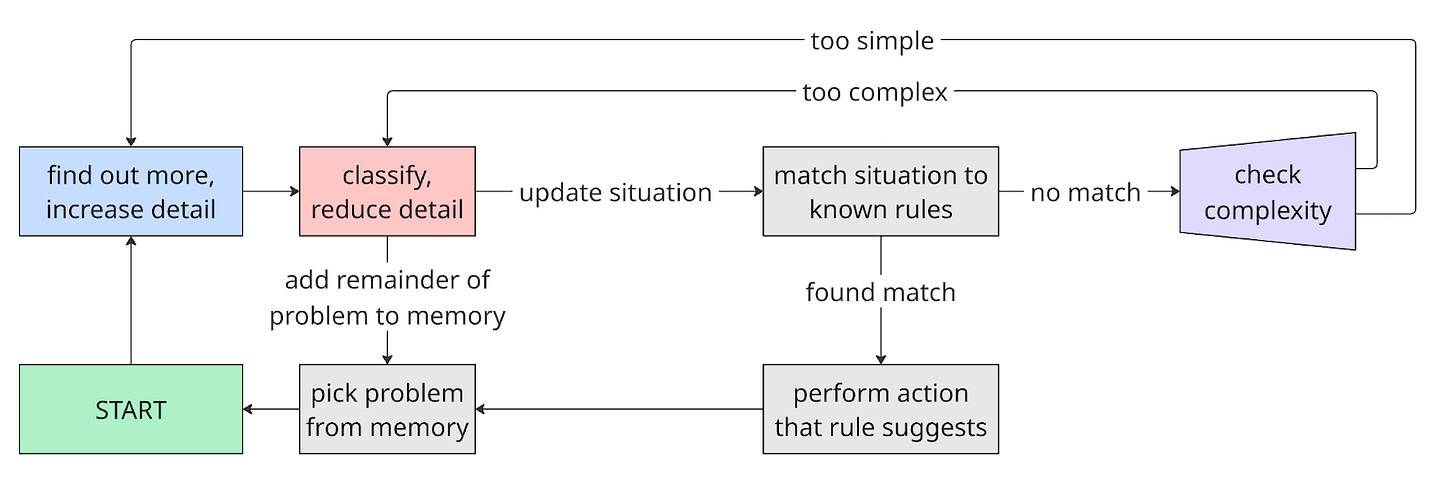
Abstraction is how we can deal with complexity—by replacing a system with a model of the system, you only care about its inputs and outputs, ignoring the rest. If something is too complex, you can always choose to care about less.
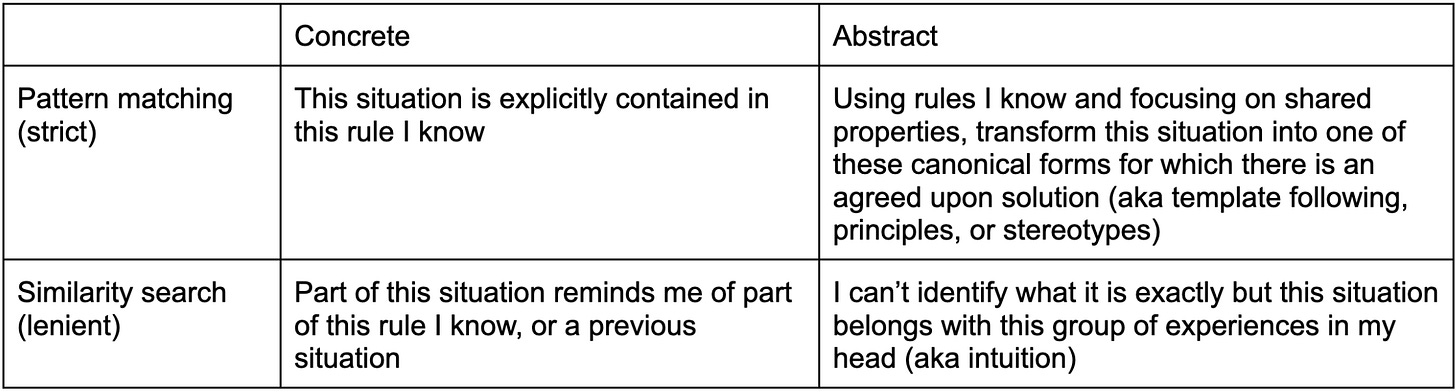
We use varying levels of abstraction for problem solving. One approach is to iteratively match parts of your situation with known rules/experiences. Either increase detail (more concrete) or decrease detail (more abstract) until your representation of the situation matches with something you can handle.
School teaches multi-level pattern matching
Almost everything I have learned in school can be described as pattern matching on varying levels of abstraction. We often start with very specific pattern matching, like how a name corresponds to the image, voice, and mannerisms of a particular person. We also have names that describe a group of things with a shared property, like how all of the following matches with “deer”:
In some way, by throwing away all of the details except for a specific property, the three following images each match exactly with “7”:
If asked to pattern match, a person identifies a common property and throws away irrelevant information. Whatever shares that common property will be matched to that pattern, regardless whether it has been seen before.
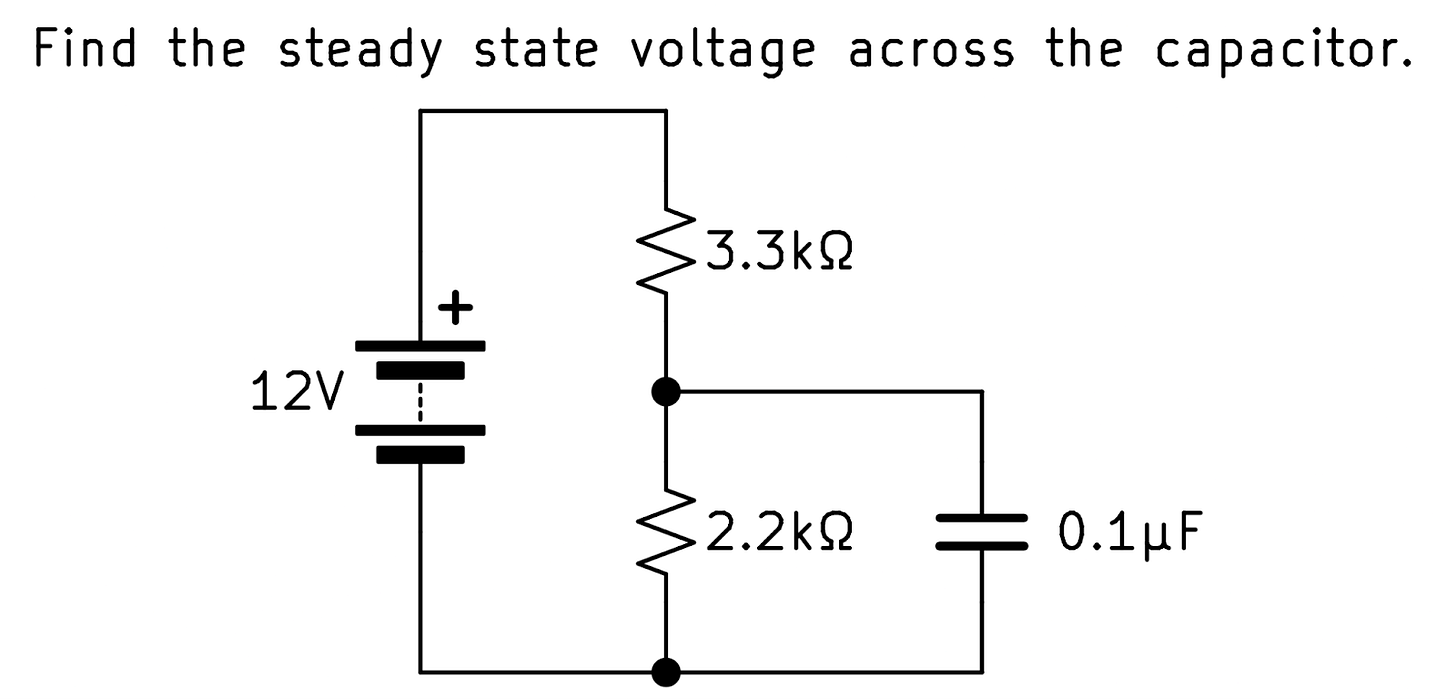
A similar process happens during problem solving, where the matching happens on the level of rules and strategies. My engineering classes often involved tasks of this style:
There are some direct pattern matches:
The symbol labeled 12V is a battery.
The squiggly lines labeled 3.3kΩ and 2.2kΩ are resistors.
The parallel plate labeled 0.1μF is a capacitor .
What we learn in lecture are rules like:
When analyzing circuits, label something as 0V. The bottom side of the battery usually makes sense.
Current into a node equals current out of the node.
Voltage across a resistor follows this rule: v = i*R.
Voltage across a battery is assumed constant at the voltage it is labeled.
In steady state, assume no current across a capacitor.
In steady state, assume no voltage across an inductor.
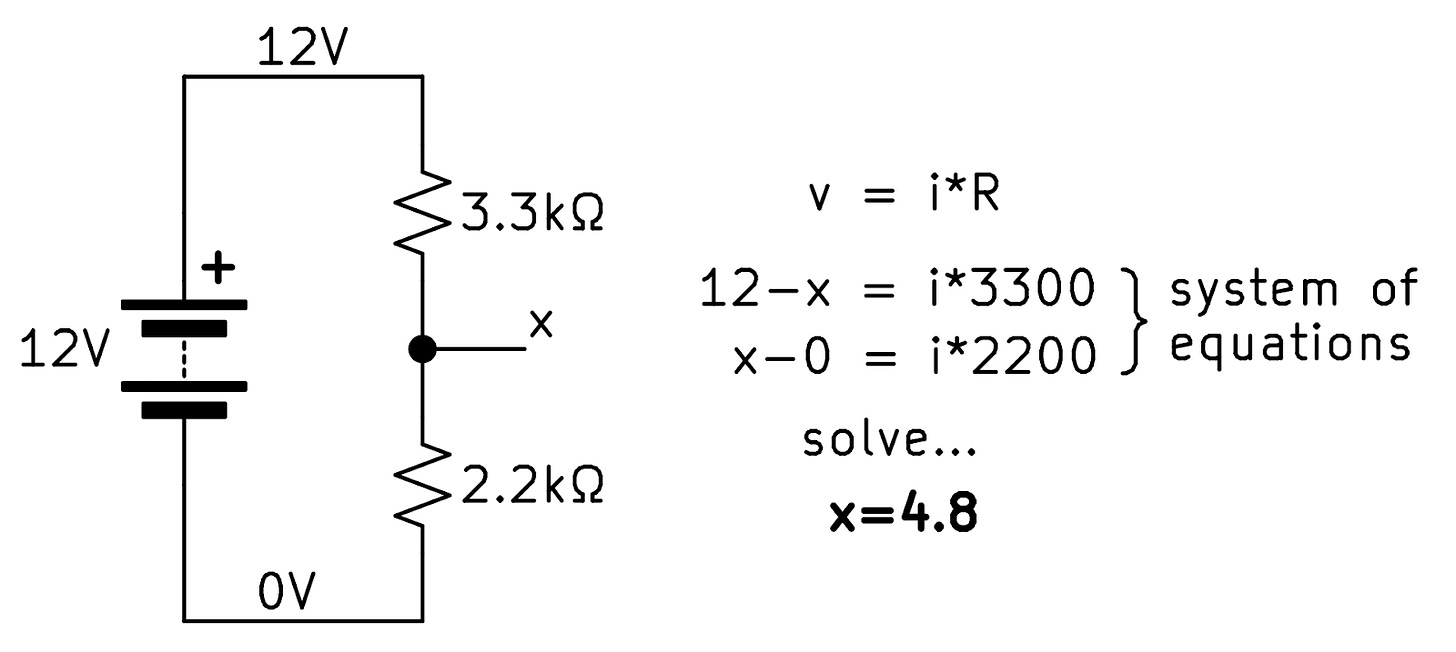
One way of solving resistor circuits is to write v=i*R for every resistor, which results in a system of equations.
All of the above rules except for the one about inductors can be exactly matched and applied to the current problem. There are likely many other rules stored in the mind of the problem solver, so I think the main challenge of learning to solve problems like these is searching for which known rules can be matched to the current problem. Finding what info is important is a critical part of the process, and this is what pattern matching is for.
Once the problem solver is more familiar, they may instead match the “structure” of the problem with a particular set of rules commonly used for other problems of this “structure”—a higher level of abstraction. In some cases, the process of recognizing these structures or canonical forms are directly taught; in other cases, these shortcuts are built up over practice. Here, the circuit has a voltage divider structure, where the voltage across the bottom resistor can be simply computed with:
Complexity is reduced by caring about fewer details, like the current through the resistors. Matching the problem to one structure and then to one rule is faster than matching many components to a whole list of component-level rules. Operating with more abstraction may be less prone to error because there are fewer steps.
On every level of familiarity though, this kind of problem solving is some sort of pattern matching, either to explicit rules or intuitions about strategies, and it can be emulated on a computer with a large enough table of definitions, rules, and strategies, plus a good way to query them. This is what expert systems do. The issue for computers is that it takes a long time for a programmer to explicitly define all these rules manually, and the issue for humans is that it’s hard to remember all the rules, plus it takes a ton of practice to be efficient at searching for relevant rules.
A more flexible form: Reasoning is multi-level similarity search
What we learn in school is primarily (multi-level) pattern matching. But I think in practice, reasoning becomes a more general form that is similarity search, which softens some of the constraints and allows for problem solving in unique cases where previous experiences are only vaguely relevant.
The pattern matching I wrote about in the last section can be compared to something like regex. A string of text must satisfy a set of properties in order to match to a particular pattern. Once properly matched, there is no question that the match is correct.
This regex can be used to search for strings that follow the email address format.
In school problems have to be graded, which means they must have clear correct answers and all the necessary information must be already available in the question. There is guaranteed at least one match, so we get used to being able to use strict filters all the time. In other words, my technical classes focused on rigorous, “perfect match” reasoning where assumptions must be met in order to move on. To be objectively verifiable was the ideal.
Having spent too much time in engineering school, I used to think that all useful reasoning could be represented by pattern matching. If it can’t be pattern matched, I just haven’t learned enough. I realized, however, that there was a disconnect between my approach for homework and my approach for real, context-full problems I encountered during my time away from school. Real problems (engineering or not) actually involve a lot of fuzzy matching, where you never can find all the information necessary, there is no guarantee that there would be an exact match between the current situation and your past experience, and the choice you eventually make is rarely objectively verifiable. This is when strict pattern matching becomes lenient similarity search. To complete the analogy, a Google search is more lenient than regex, but a human expert is more lenient than both, being able to suggest connections whose relevance is defined by a type of similarity that transcends keywords.
Computers are awfully good at perfect pattern-matching. Skills with more literal pattern-matching like arithmetic and grammar were first solved with computers compared to skills that require fuzzier similarity search like detecting tone in language or coming up with new math proofs. Computers were too good at following rules up until recently, but then we gave them a bunch of data (much of which is probably not relevant to any individual problem), and because the data was so big, we had to give them a way of fuzzy querying using continuous “distances” between words instead of using strict filters: methods with probabilities and estimated expected values instead of rules and templates. I think that it’s not just the absolute amount of the data, but also this softening of constraints, the widening from pattern matching to similarity search, is why current large language model reasoning seems so much closer to our own and expanded capabilities as much as it did.
Language is limited, so harder to teach ≠ harder to learn
I think there’s a perception that moving from concrete to abstract or moving from rule-following to flexible reasoning is a step up in difficulty. It seems that way because teachers generally try to use straightforward language (so that the student is sure to have the same idea; the information is transferred without error) which struggles with the abstract and the imprecise. However, I don’t think that making abstractions or unclear connections are inherently harder skills, we just find it harder to explicitly teach. In fact, people generalize using stereotypes and reason using vague personal anecdotes all the time, maybe even too much. It’s a limitation of our language that makes it hard to convey the thought process behind far-reaching connections, because language is a compression algorithm.
Unlike thought, language is linear—writers gather their tangled cotton clouds and spin it to thread—a line of reasoning. Compression algorithms always assume some shared background knowledge or context; to be understood, encoders need a corresponding decoder. As a listener or reader, you are constantly predicting possible meanings of a sentence before it even finishes, so what the sentence does at the time it is complete is that it simply allows you to choose which one of your interpretations it matches the most. Uncommon connections are hard to predict, like how there are more ways to break a rule than to follow one.
Similarly, a student having grasped the “foundations” make them easier to teach because the teacher (whether a person, book, or other content) knows what existing knowledge can be connected to the topic at hand. It’s possible to use straightforward language to convey directions from their shared starting point to the new topic. However, as I argue in the towers post, the new topic is not necessarily harder to learn than those that the person picked up before. Connections go both ways like hiking trails, and difficulty depends on where you start. My point here is that harder to teach does not always mean harder to learn, if the student can learn through experience or has diverse enough teachers.
By itself, intuition is not hard, and logic at its core (without layers and layers of notation and definitions) is obvious. It is hard, however, to reason at the speed of intuition but with the verifiability of logic, since then you need to layer them alternatively on top of each other.
Alternating between abstractions can unblock creativity
There is a theory that imagination follows a path of least resistance: “the default approach in tasks of imagination is to access a specific known entity or category exemplar and pattern the new entity after it” (This and other ideas in this section come from The Creative Cognition Approach). But directly using a known pattern rarely results in something truly innovative. There are two very different ways of suppressing the default of deriving from common examples: either add specific constraints that disallow common examples, or remove constraints by abstracting away everything but a purpose.
Original: Design a better grocery bag.
Concrete constraints: What can you create with only the following material? Twine, cereal boxes, socks.
More abstracted: What are ways to transport a collection of squishy items from the store to the home?
Original: Paint a fish.
Concrete constraints: Paint a fish using only colors found on this piece of paper.
More abstracted: Depict a water creature that looks dumb enough it would be considered ethical to hunt them for human enjoyment.
Interestingly, the more abstracted prompt is longer and seems like it contains more detail, because it calls to attention a property of the original subject that may not be considered when described by a common, shorter word. Both methods better define the problem (adds information) by moving away from the default level of abstraction.
Moving up and down abstraction levels can be treated as a control problem—we get to choose at what level we want to think. We might sometimes get stuck on a problem at a certain level of abstraction, and alternatively adding or removing constraints is a way of forcing or pruning the relevance of certain prior experiences that can unblock new directions for brainstorming. 1
Art helps us find what we want to optimize
This section is inspired by actor-critic reinforcement learning.
I can’t stop thinking about robots, so this will be another robotics analogy. I’ll compare different strategies of controlling dynamical systems with their level of abstraction. Let’s say we want to make an upright robot stay upright:
At the lowest level we can have a dense lookup table: a big list of instances, particular inputs map to particular outputs. “If falling forward 5 degrees, lean back with 1 unit of effort; if falling forward 10 degrees, lean back with 2 units of effort; if falling backwards 10 degrees, lean forward with 2 units of effort...”. To adjust, update each entry in the table manually.
Going one layer of abstraction higher are rules/relationships/policies, writing down not each instance but a formula like: “balance_effort = -0.2 * body_angle”. Not as flexible as the lookup table, but it can describe strategies using less storage, a kind of information compression. You assume there’s some computer in place that can evaluate the formula. From the learning perspective, this is like finding a pattern so you need to remember less. To adjust, update the coefficient -0.2.
Value functions are at a higher layer: “it’s good if body_angle is close to 0”. The only information you really store is a proxy for the goal, and you assume there’s some optimization algorithm in place that searches for the right policy that pushes the value function in the desirable direction. It’s as if there’s a person inside with their hand on the controls, and they just need to know what’s good and what’s bad. To adjust, update the value function to something else like “it’s good if {some other thing} is close to {value}”.
Sometimes capable people can collaborate just by aligning their value functions, without the need of going into implementation details of policies or instances. It might not be the best way to collaborate, but it works because they trust each others’ intentions and their optimizers.
Value functions are not exactly the same as a goal or a reward. A value function can be evaluated at any time to determine a single number describing the “goodness” of a situation. How much do I like this? In contrast, a goal could be vague like “I want the robot to balance” and rewards usually come from the outside, intermittently and maybe randomly, like “if the robot balances for long enough people will praise it”. Good value functions are internal and learned through experience. They will often be able to anticipate (“this situation is nice, feels like I can expect a reward soon”), so they help with choosing between two potential actions: which hypothetical result has a better value? Without a good value function, even a good optimizer can be ineffective or dangerous. See Goodhart’s law and paperclip maximizers. 2
I don’t like it when there are too many definitions but I bring up value functions because I think it describes a connection I like between art and engineering. I think experiencing and creating art makes us develop taste, which is (maybe among other things) a standard by which we evaluate how much we like something. In other words, taste is a value function, a proxy for happiness, fulfillment, and other life goals. By having different learned tastes, we each optimize our creations in our own unique direction.
“Art is meant to disturb, science reassures” - painter Georges Braque
“Art asks questions, engineering answers them” - roboticist/artist Dennis Hong
“Art refines our inner critic, engineering satisfies it” - an oversimplification by me
A cool phenomenon is that diversity doesn’t necessarily improve performance on existing metrics but rather creates an opportunity to improve the metric itself, which is arguably more important. The most useful thing of working with people of different backgrounds in my opinion is learning their preferences and what they consider to be most important. It’s like the difference between exploitation, which allows you to move faster in the direction you want, and exploration, which allows you to find the direction you actually want. Again, I’m in favor of an alternating strategy: exploration and exploitation, art and engineering, value functions and optimization.3 While crossing the street, keep looking both ways.
Summary
Wow, that was one of the longest things I’ve ever written. It should probably be split into multiple essays. The points I make above are held together weakly by the shared concept of abstractions, and how regulating its level can help us optimize for the right things, be more creative, simplify complex systems, and solve problems entirely by finding new ways two things are similar.
Thank you to friends and family for the conversations that led to the opinions that I share here. These opinions are influenced too by my experiences in and out of a school mindset (what I gained the most from that gap semester was the really the contrasts during transitions), so thank you also to everyone who made that possible.
For more on adding and removing constraints to help creativity, see the Geneplore model
By the way, I think robots with human-like features are a good intermediate step—but are not the end solution—towards to introducing more intelligent robots into our society, because we have a convenient value function to evaluate their capability. Can it do the things humans do in a way humans do?
Someone did a PhD thesis on mathematically optimizing how often to switch strategies during problem solving